30
ENGINEER AND MACHINIST’S DRAWING-BOOK.
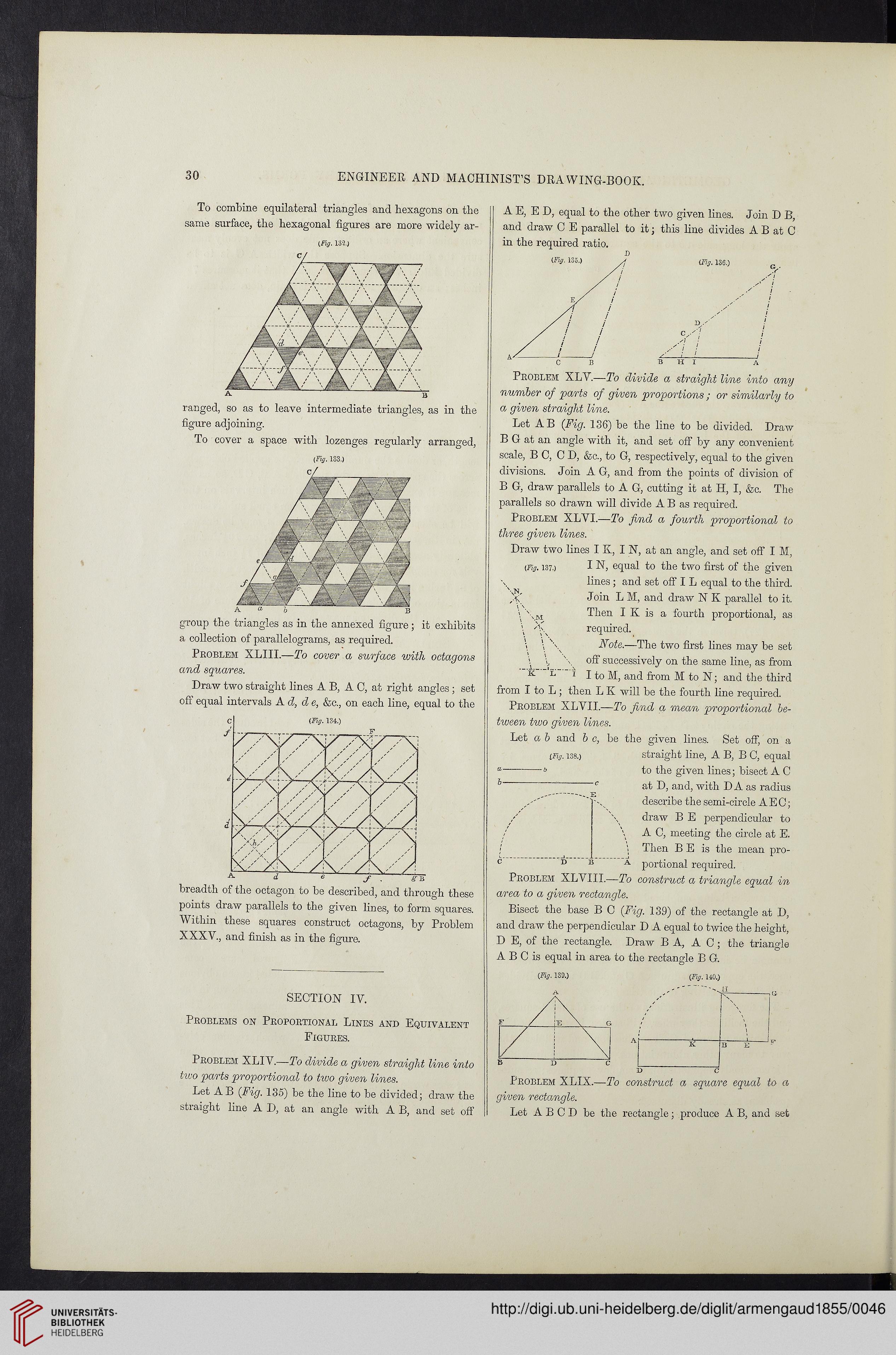
To combine equilateral triangles and hexagons on the
same surface, the hexagonal figures are more widely ar-
(Fig. 132.)
-V-
-V --
B*
ranged, so as to leave intermediate triangles, as in the
figure adjoining.
To cover a space with lozenges regularly arranged,
(Fig. 133.)
c/
A. a b B
group the triangles as in the annexed figure ; it exhibits
a collection of parallelograms, as required.
Problem XLIII.—To cover a surface with octagons
and squares.
Draw two straight lines A B, AC, at right angles ; set
off equal intervals A cl, cl e, &c., on each line, equal to the
breadth of the octagon to be described, and through these
points draw parallels to the given lines, to form squares.
Within these squares construct octagons, by Problem
XXXV., and finish as in the figure.
SECTION IV.
Problems on Proportional Lines and Equivalent
Figures.
Problem XLIV.—To divide a given straight line into
two 'parts proportional to two given lines.
Let AB {Fig. 135) be the line to be divided; draw the
straight line A D, at an angle with A B, and set off
A E, E D, equal to the other two given lines. Join D B,
and draw C E parallel to it; this fine divides A B at C
in the required ratio.
{Fig. 136.)
Problem XLV.—To divide a straight line into any
number of parts of given proportions ; or similarly to
a given straight line.
Let AB (Fig. 136) be the line to be divided. Draw
B G at an angle with it, and set off by any convenient
scale, B C, CD, &c., to G, respectively, equal to the given
divisions. Join AG, and from the points of division of
B G, draw parallels to A G, cutting it at H, I, &c. The
parallels so drawn will divide A B as required.
Problem XLVI.—To find a fourth proportional to
three given lines.
Draw two lines I K, I N, at an angle, and set off I M,
(Fig. 137.)
I N, equal to the two first of the given
lines ; and set off I L equal to the third.
\N.
Join L M, and draw N K parallel to it.
\ \
\
Then I K is a fourth proportional, as
'■ '\
required.
{Fig. 138.)
-E
V-
\ \ \ Note.—The two first lines may be set
\, \ off successively on the same line, as from
K ^ 1 I to M, and from M to N; and the third
from I to L ; then L K will be the fourth line required.
Problem XLVII.—To find a mean proportional be-
tween tivo given lines.
Let a b and b c, be the given lines. Set off, on a
straight line, A B, B C, equal
to the given lines; bisect A C
at D, and, with D A as radius
describe the semi-circle A EC;
draw B E perpendicular to
A C, meeting the circle at E.
• Then B E is the mean pro-
c dba portional required.
Problem XLVIII.—To construct a triangle equal in
area to a given rectangle.
Bisect the base B C (Fig. 139) of the rectangle at D,
and draw the perpendicular D A equal to twice the height,
D E, of the rectangle. Draw BA, AC; the triangle
A B C is equal in area to the rectangle B G.
(Fig. 139.) (Fig. 11-0.)
/
\
>
1
K
B E
Problem XLIX.—To construct a square equcd to a
given rectangle.
Let A B C D be the rectangle; produce A B, and set
ENGINEER AND MACHINIST’S DRAWING-BOOK.
To combine equilateral triangles and hexagons on the
same surface, the hexagonal figures are more widely ar-
(Fig. 132.)
-V-
-V --
B*
ranged, so as to leave intermediate triangles, as in the
figure adjoining.
To cover a space with lozenges regularly arranged,
(Fig. 133.)
c/
A. a b B
group the triangles as in the annexed figure ; it exhibits
a collection of parallelograms, as required.
Problem XLIII.—To cover a surface with octagons
and squares.
Draw two straight lines A B, AC, at right angles ; set
off equal intervals A cl, cl e, &c., on each line, equal to the
breadth of the octagon to be described, and through these
points draw parallels to the given lines, to form squares.
Within these squares construct octagons, by Problem
XXXV., and finish as in the figure.
SECTION IV.
Problems on Proportional Lines and Equivalent
Figures.
Problem XLIV.—To divide a given straight line into
two 'parts proportional to two given lines.
Let AB {Fig. 135) be the line to be divided; draw the
straight line A D, at an angle with A B, and set off
A E, E D, equal to the other two given lines. Join D B,
and draw C E parallel to it; this fine divides A B at C
in the required ratio.
{Fig. 136.)
Problem XLV.—To divide a straight line into any
number of parts of given proportions ; or similarly to
a given straight line.
Let AB (Fig. 136) be the line to be divided. Draw
B G at an angle with it, and set off by any convenient
scale, B C, CD, &c., to G, respectively, equal to the given
divisions. Join AG, and from the points of division of
B G, draw parallels to A G, cutting it at H, I, &c. The
parallels so drawn will divide A B as required.
Problem XLVI.—To find a fourth proportional to
three given lines.
Draw two lines I K, I N, at an angle, and set off I M,
(Fig. 137.)
I N, equal to the two first of the given
lines ; and set off I L equal to the third.
\N.
Join L M, and draw N K parallel to it.
\ \
\
Then I K is a fourth proportional, as
'■ '\
required.
{Fig. 138.)
-E
V-
\ \ \ Note.—The two first lines may be set
\, \ off successively on the same line, as from
K ^ 1 I to M, and from M to N; and the third
from I to L ; then L K will be the fourth line required.
Problem XLVII.—To find a mean proportional be-
tween tivo given lines.
Let a b and b c, be the given lines. Set off, on a
straight line, A B, B C, equal
to the given lines; bisect A C
at D, and, with D A as radius
describe the semi-circle A EC;
draw B E perpendicular to
A C, meeting the circle at E.
• Then B E is the mean pro-
c dba portional required.
Problem XLVIII.—To construct a triangle equal in
area to a given rectangle.
Bisect the base B C (Fig. 139) of the rectangle at D,
and draw the perpendicular D A equal to twice the height,
D E, of the rectangle. Draw BA, AC; the triangle
A B C is equal in area to the rectangle B G.
(Fig. 139.) (Fig. 11-0.)
/
\
>
1
K
B E
Problem XLIX.—To construct a square equcd to a
given rectangle.
Let A B C D be the rectangle; produce A B, and set