THE PROJECTION OF SHADOWS.
83
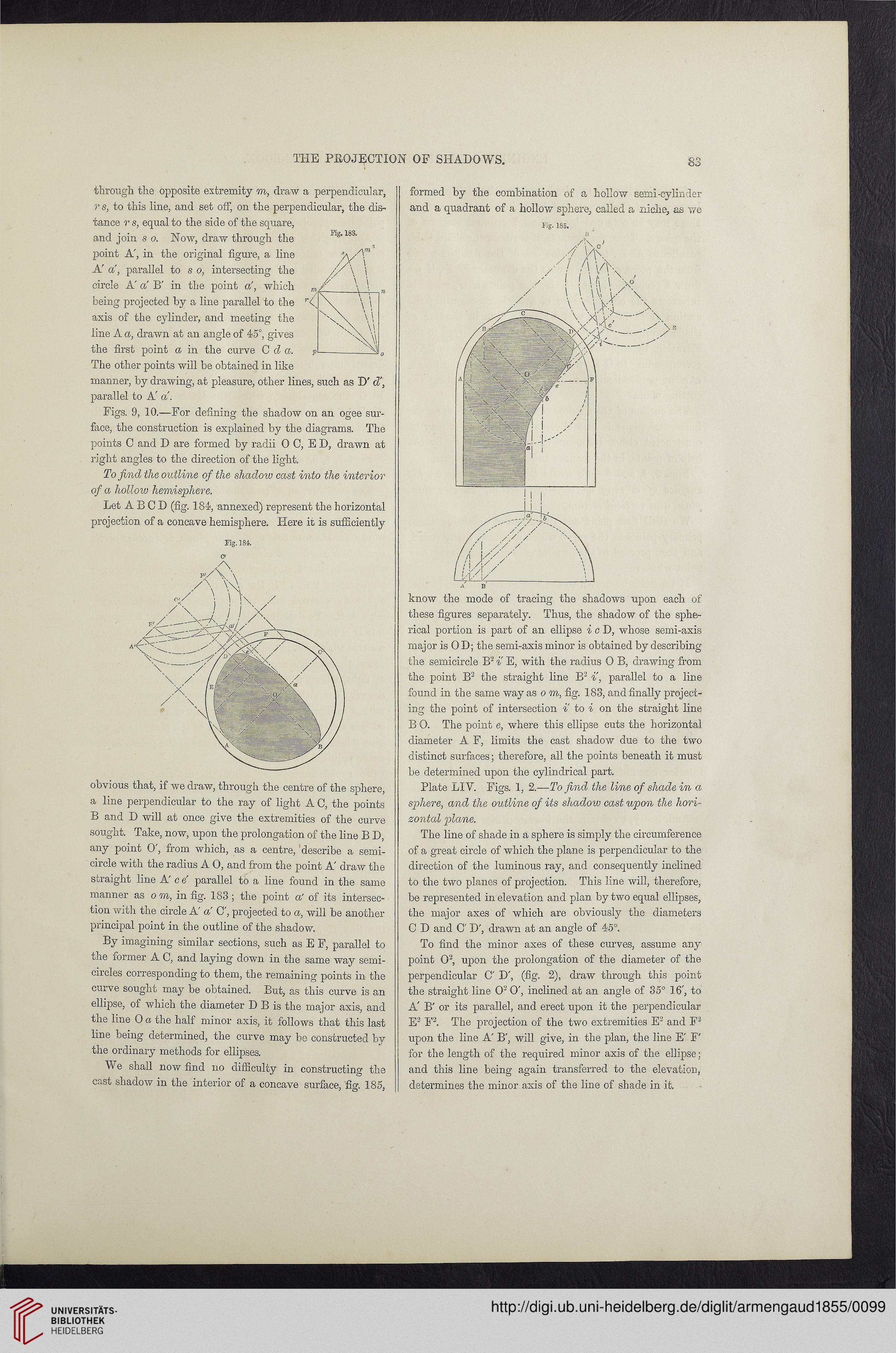
through the opposite extremity to, draw a perpendicular,
r s, to this line, and set off, on the perpendicular, the dis-
tance r s, equal to the side of the square,
and join s o. Now, draw through the
point A', in the original figure, a line
A' a, parallel to s o, intersecting the
circle A' a B' in the point a, which
being projected by a line parallel to the r
axis of the cylinder, and meeting the
line A a, drawn at an angle of 45°, gives
the first point a in the curve C da.
The other points will be obtained in like
manner, by drawing, at pleasure, other lines, such as D'd',
parallel to A' a.
Figs. 9, 10.—For defining the shadow on an ogee sur-
face, the construction is explained by the diagrams. The
points C and D are formed by radii 0 C, E D, drawn at
right angles to the direction of the light.
To find the outline of the shadow cast into the interior
of a hollow hemisphere.
Let A B C D (fig. 184, annexed) represent the horizontal
projection of a concave hemisphere. Here it is sufficiently
Tig. 184.
C'
obvious that, if we draw, through the centre of the sphere,
a line perpendicular to the ray of light A C, the points
B and D will at once give the extremities of the curve
sought. Take, now, upon the prolongation of the line B D,
any point O', from which, as a centre, describe a semi-
circle with the radius A O, and from the point A' draw the
straight line A' c e' parallel to a line found in the same
manner as oto, in fig. 183; the point a' of its intersec-
tion with the circle A' a O', projected to a, will be another
principal point in the outline of the shadow.
By imagining similar sections, such as E F, parallel to
the former A C, and laying down in the same way semi-
circles corresponding to them, the remaining points in the
curve sought may be obtained. But, as this curve is an
ellipse, of which the diameter D B is the major axis, and
the line 0 a the half minor axis, it follows that this last
line being determined, the curve may be constructed bv
the ordinary methods for ellipses.
We shall now find no difficulty in constructing the
cast shadow in the interior of a concave surface, fig. 185,
formed by the combination of a hollow semi-cylinder
and a quadrant of a hollow sphere, called a niche, as we
Fig. 185.
IS
know the mode of tracing the shadows upon each of
these figures separately. Thus, the shadow of the sphe-
rical portion is part of an ellipse i cD, whose semi-axis
major is OD; the semi-axis minor is obtained by describing
the semicircle B2 % E, with the radius 0 B, drawing from
the point B2 the straight line B2 i', parallel to a line
found in the same way as o to, fig. 183, and finally project-
ing the point of intersection i' to i on the straight line
B O. The point e, where this ellipse cuts the horizontal
diameter A F, limits the cast shadow due to the two
distinct surfaces; therefore, all the points beneath it must
be determined upon the cylindrical part.
Plate LI V. Figs. 1, 2.—To find the line of shade in a
sphere, and the outline of its shadow cast upon the hori-
zontal plane.
The line of shade in a sphere is simply the circumference
of a great circle of which the plane is perpendicular to the
direction of the luminous ray, and consequently inclined
to the two planes of projection. This line will, therefore,
be represented in elevation and plan by two equal ellipses,
the major axes of which are obviously the diameters
C D and C' D', drawn at an angle of 45°.
To find the minor axes of these curves, assume any
point O2, upon the prolongation of the diameter of the
perpendicular C' D', (fig. 2), draw through this point
the straight line O2 O', inclined at an angle of 35° 16', to
A' B' or its parallel, and erect upon it the perpendicular
E2 F2. The projection of the two extremities E2 and F2
upon the line A' B', will give, in the plan, the line E' F'
for the length of the required minor axis of the ellipse;
and this line being again transferred to the elevation,
determines the minor axis of the line of shade in it.
83
through the opposite extremity to, draw a perpendicular,
r s, to this line, and set off, on the perpendicular, the dis-
tance r s, equal to the side of the square,
and join s o. Now, draw through the
point A', in the original figure, a line
A' a, parallel to s o, intersecting the
circle A' a B' in the point a, which
being projected by a line parallel to the r
axis of the cylinder, and meeting the
line A a, drawn at an angle of 45°, gives
the first point a in the curve C da.
The other points will be obtained in like
manner, by drawing, at pleasure, other lines, such as D'd',
parallel to A' a.
Figs. 9, 10.—For defining the shadow on an ogee sur-
face, the construction is explained by the diagrams. The
points C and D are formed by radii 0 C, E D, drawn at
right angles to the direction of the light.
To find the outline of the shadow cast into the interior
of a hollow hemisphere.
Let A B C D (fig. 184, annexed) represent the horizontal
projection of a concave hemisphere. Here it is sufficiently
Tig. 184.
C'
obvious that, if we draw, through the centre of the sphere,
a line perpendicular to the ray of light A C, the points
B and D will at once give the extremities of the curve
sought. Take, now, upon the prolongation of the line B D,
any point O', from which, as a centre, describe a semi-
circle with the radius A O, and from the point A' draw the
straight line A' c e' parallel to a line found in the same
manner as oto, in fig. 183; the point a' of its intersec-
tion with the circle A' a O', projected to a, will be another
principal point in the outline of the shadow.
By imagining similar sections, such as E F, parallel to
the former A C, and laying down in the same way semi-
circles corresponding to them, the remaining points in the
curve sought may be obtained. But, as this curve is an
ellipse, of which the diameter D B is the major axis, and
the line 0 a the half minor axis, it follows that this last
line being determined, the curve may be constructed bv
the ordinary methods for ellipses.
We shall now find no difficulty in constructing the
cast shadow in the interior of a concave surface, fig. 185,
formed by the combination of a hollow semi-cylinder
and a quadrant of a hollow sphere, called a niche, as we
Fig. 185.
IS
know the mode of tracing the shadows upon each of
these figures separately. Thus, the shadow of the sphe-
rical portion is part of an ellipse i cD, whose semi-axis
major is OD; the semi-axis minor is obtained by describing
the semicircle B2 % E, with the radius 0 B, drawing from
the point B2 the straight line B2 i', parallel to a line
found in the same way as o to, fig. 183, and finally project-
ing the point of intersection i' to i on the straight line
B O. The point e, where this ellipse cuts the horizontal
diameter A F, limits the cast shadow due to the two
distinct surfaces; therefore, all the points beneath it must
be determined upon the cylindrical part.
Plate LI V. Figs. 1, 2.—To find the line of shade in a
sphere, and the outline of its shadow cast upon the hori-
zontal plane.
The line of shade in a sphere is simply the circumference
of a great circle of which the plane is perpendicular to the
direction of the luminous ray, and consequently inclined
to the two planes of projection. This line will, therefore,
be represented in elevation and plan by two equal ellipses,
the major axes of which are obviously the diameters
C D and C' D', drawn at an angle of 45°.
To find the minor axes of these curves, assume any
point O2, upon the prolongation of the diameter of the
perpendicular C' D', (fig. 2), draw through this point
the straight line O2 O', inclined at an angle of 35° 16', to
A' B' or its parallel, and erect upon it the perpendicular
E2 F2. The projection of the two extremities E2 and F2
upon the line A' B', will give, in the plan, the line E' F'
for the length of the required minor axis of the ellipse;
and this line being again transferred to the elevation,
determines the minor axis of the line of shade in it.