PERSPECTIVE.
115
jection of one of the diagonals of each face of the cube,
and consequently one of the diameters of the circle, is of
the same size as the original, we have at once the major
axis of the ellipse which the projection of the circle forms,
and as the circle touches each side of the square, we have
also four points in the circumference of the ellipse, and we
have only to find the isometric projection of its minor axis.
From the intersections of the diagonals of the faces of the
cube, set off on the major axis the radius of the circle at
abed ef, and through the points thus obtained draw
isometric lines cutting the minor axes in 1, 2, 3, 4, 5, 6,
and we thus obtain the length of the minor axis. The
ellipse can then be sketched by hand, or trammelled by a
slip of paper.
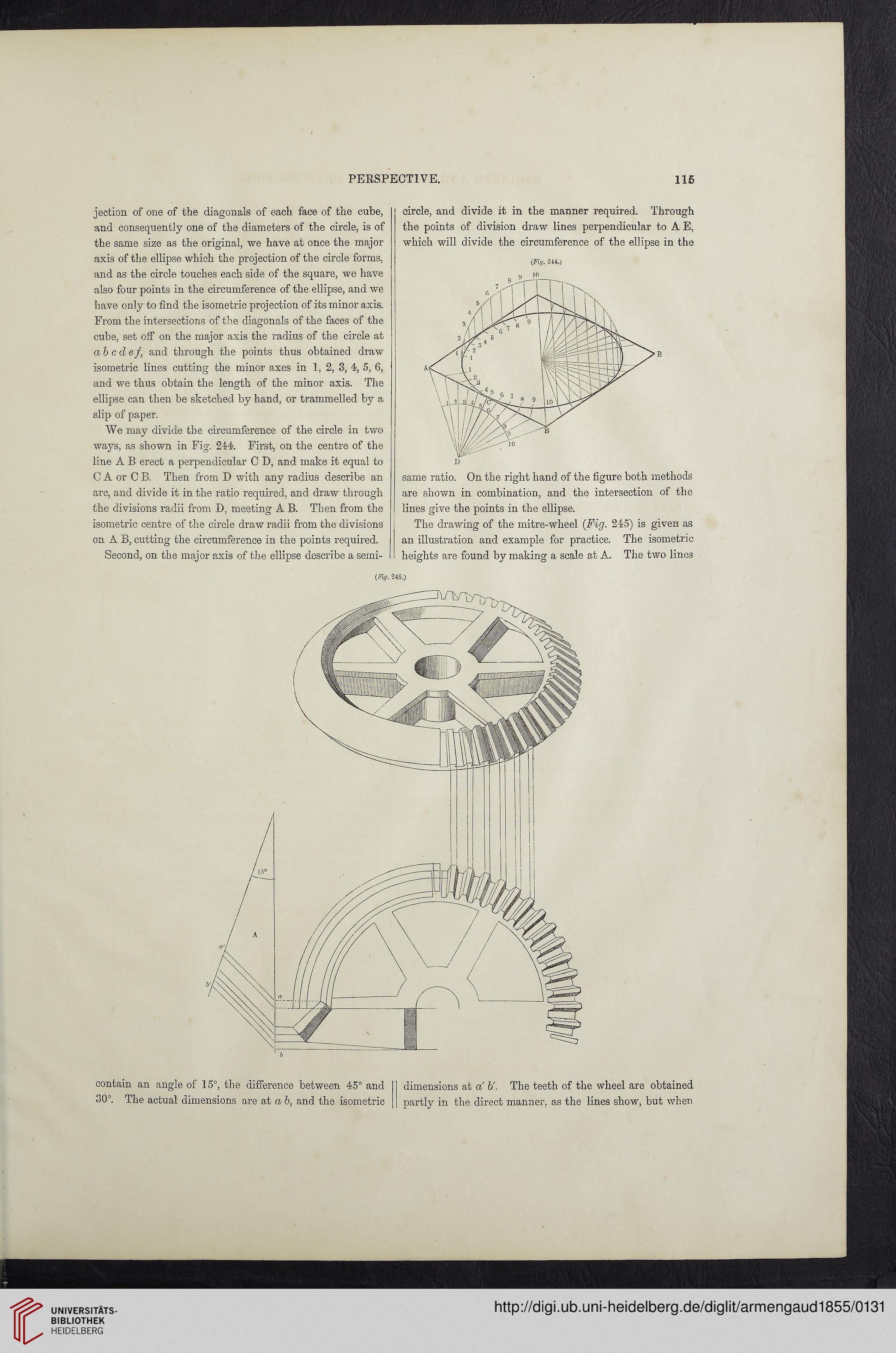
We may divide the circumference of the circle in two
ways, as shown in Fig. 244. First, on the centre of the
line A B erect a perpendicular C D, and make it equal to
C A or C B. Then from I) with any radius describe an
arc, and divide it in the ratio required, and draw through
the divisions radii from D, meeting A B. Then from the
isometric centre of the circle draw radii from the divisions
on A B, cutting the circumference in the points required.
Second, on the major axis of the ellipse describe a semi-
circle, and divide it in the manner required. Through
the points of division draw lines perpendicular to A E,
which will divide the circumference of the ellipse in the
(Fig. 2440
same ratio. On the right hand of the figure both methods
are shown in combination, and the intersection of the
lines give the points in the ellipse.
The drawing of the mitre-wheel (Fig. 245) is given as
an illustration and example for practice. The isometric
heights are found by making a scale at A. The two lines
(Fig. 245.)
contain an angle of 15°, the difference between 45° and
30°. The actual dimensions are at a b, and the isometric
dimensions at a b'. The teeth of the wheel are obtained
partly in the direct manner, as the lines show, but when
115
jection of one of the diagonals of each face of the cube,
and consequently one of the diameters of the circle, is of
the same size as the original, we have at once the major
axis of the ellipse which the projection of the circle forms,
and as the circle touches each side of the square, we have
also four points in the circumference of the ellipse, and we
have only to find the isometric projection of its minor axis.
From the intersections of the diagonals of the faces of the
cube, set off on the major axis the radius of the circle at
abed ef, and through the points thus obtained draw
isometric lines cutting the minor axes in 1, 2, 3, 4, 5, 6,
and we thus obtain the length of the minor axis. The
ellipse can then be sketched by hand, or trammelled by a
slip of paper.
We may divide the circumference of the circle in two
ways, as shown in Fig. 244. First, on the centre of the
line A B erect a perpendicular C D, and make it equal to
C A or C B. Then from I) with any radius describe an
arc, and divide it in the ratio required, and draw through
the divisions radii from D, meeting A B. Then from the
isometric centre of the circle draw radii from the divisions
on A B, cutting the circumference in the points required.
Second, on the major axis of the ellipse describe a semi-
circle, and divide it in the manner required. Through
the points of division draw lines perpendicular to A E,
which will divide the circumference of the ellipse in the
(Fig. 2440
same ratio. On the right hand of the figure both methods
are shown in combination, and the intersection of the
lines give the points in the ellipse.
The drawing of the mitre-wheel (Fig. 245) is given as
an illustration and example for practice. The isometric
heights are found by making a scale at A. The two lines
(Fig. 245.)
contain an angle of 15°, the difference between 45° and
30°. The actual dimensions are at a b, and the isometric
dimensions at a b'. The teeth of the wheel are obtained
partly in the direct manner, as the lines show, but when