DOI issue:
Originalbeiträge
DOI article:Grebe, C.: Die Hauptrastertypen
DOI Page / Citation link:https://doi.org/10.11588/diglit.37611#0090
78
Die Hauptrastertypen.
und am dunkelsten hinter den opaken Theilen des Rasters
ist; dazwischen liegen verschiedene Helligkeitsgrade.
Als Lichtquelle fungirt die Blendenfläche, deren Hellig-
keit proportional der Lichtstärke der entsprechenden Object-
punkte variirt.
Bezeichnet man mit J die Beleuchtung auf den Theilen
der Bildebene, welche den vollen Betrag der Blendenhellig-
keit empfangen, mit q den Theil der von einem Punkte des
Halbschattens aus sichtbaren Blendenöffnung, so ist die Be-
leuchtung i in diesem Punkte
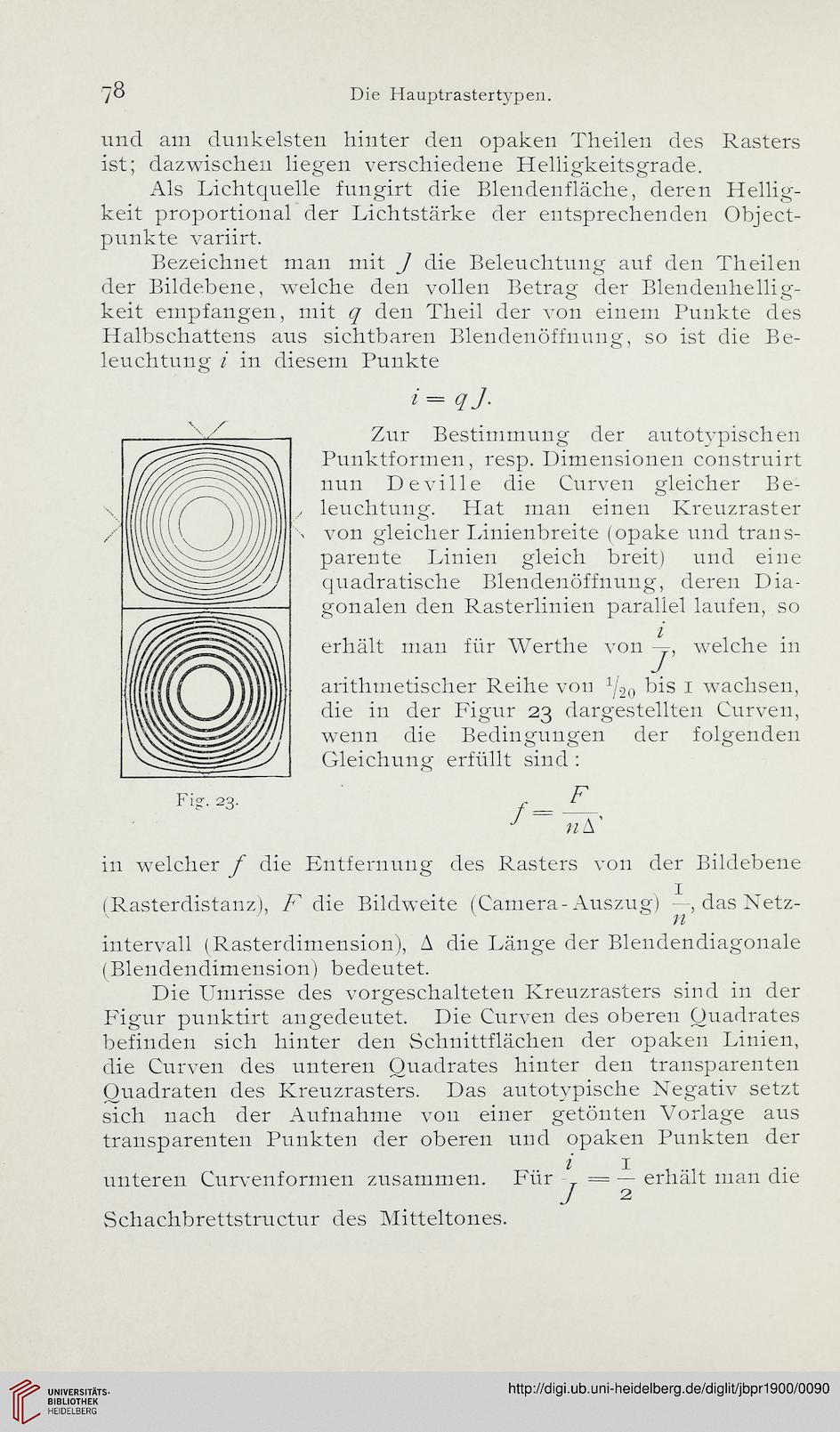
Fig. 23.
7= qj.
Zur Bestimmung der autotypischen
Punktformen, resp. Dimensionen construirt
nun Deville die Curven gleicher Be-
leuchtung. Hat man einen Kreuzraster
von gleicher Linienbreite (opake und trans-
parente Linien gleich breit) und eine
quadratische Blendenöffnung, deren Dia-
gonalen den Rasterlinien parallel laufen, so
i
erhält man für Werthe von y, welche in
arithmetischer Reihe von 1/.2O bis 1 wachsen,
die in der Figur 23 dargestellten Curven,
wenn die Bedingungen der folgenden
Gleichung erfüllt sind :
in welcher f die Entfernung des Rasters von der Bildebene
(Rasterdistanz), F die Bildweite (Camera-Auszug) —, das Netz-
intervall (Rasterdimension), A die Länge der Blendendiagonale
(Blendendimension) bedeutet.
Die Umrisse des vorgeschalteten Kreuzrasters sind in der
Figur punktirt angedeutet. Die Curven des oberen Quadrates
befinden sich hinter den Schnittflächen der opaken Linien,
die Curven des unteren Quadrates hinter den transparenten
Quadraten des Kreuzrasters. Das autotypische Negativ setzt
sich nach der Aufnahme von einer getönten Vorlage aus
transparenten Punkten der oberen und opaken Punkten der
Z I
unteren Curvenformen zusammen. Für = — erhält man die
J
Schachbrettstructur des Mitteltones.
Die Hauptrastertypen.
und am dunkelsten hinter den opaken Theilen des Rasters
ist; dazwischen liegen verschiedene Helligkeitsgrade.
Als Lichtquelle fungirt die Blendenfläche, deren Hellig-
keit proportional der Lichtstärke der entsprechenden Object-
punkte variirt.
Bezeichnet man mit J die Beleuchtung auf den Theilen
der Bildebene, welche den vollen Betrag der Blendenhellig-
keit empfangen, mit q den Theil der von einem Punkte des
Halbschattens aus sichtbaren Blendenöffnung, so ist die Be-
leuchtung i in diesem Punkte
Fig. 23.
7= qj.
Zur Bestimmung der autotypischen
Punktformen, resp. Dimensionen construirt
nun Deville die Curven gleicher Be-
leuchtung. Hat man einen Kreuzraster
von gleicher Linienbreite (opake und trans-
parente Linien gleich breit) und eine
quadratische Blendenöffnung, deren Dia-
gonalen den Rasterlinien parallel laufen, so
i
erhält man für Werthe von y, welche in
arithmetischer Reihe von 1/.2O bis 1 wachsen,
die in der Figur 23 dargestellten Curven,
wenn die Bedingungen der folgenden
Gleichung erfüllt sind :
in welcher f die Entfernung des Rasters von der Bildebene
(Rasterdistanz), F die Bildweite (Camera-Auszug) —, das Netz-
intervall (Rasterdimension), A die Länge der Blendendiagonale
(Blendendimension) bedeutet.
Die Umrisse des vorgeschalteten Kreuzrasters sind in der
Figur punktirt angedeutet. Die Curven des oberen Quadrates
befinden sich hinter den Schnittflächen der opaken Linien,
die Curven des unteren Quadrates hinter den transparenten
Quadraten des Kreuzrasters. Das autotypische Negativ setzt
sich nach der Aufnahme von einer getönten Vorlage aus
transparenten Punkten der oberen und opaken Punkten der
Z I
unteren Curvenformen zusammen. Für = — erhält man die
J
Schachbrettstructur des Mitteltones.