DOI issue:
Originalbeiträge
DOI article:Pfaundler von Hadermur, Leopold: Die Zonenplatte von Soret und die Phasenumkehrplatte von Wood als Ersatz der Linse: Anwendungen derselben in der Photographie
DOI Page / Citation link:https://doi.org/10.11588/diglit.37611#0207
Die Zonenplatte von Soret u. s. w.
T95
schiedenen Stellen Q, C2 ■ ■ ■ schneiden. Wollen wir erreichen,
dass dies in einem einzigen Punkt geschehe, so müssen wir
für jedes Strahlenbündel ein anderes Prisma anwenden, dessen
brechender Winkel desto grösser ist, je weiter von der Achse
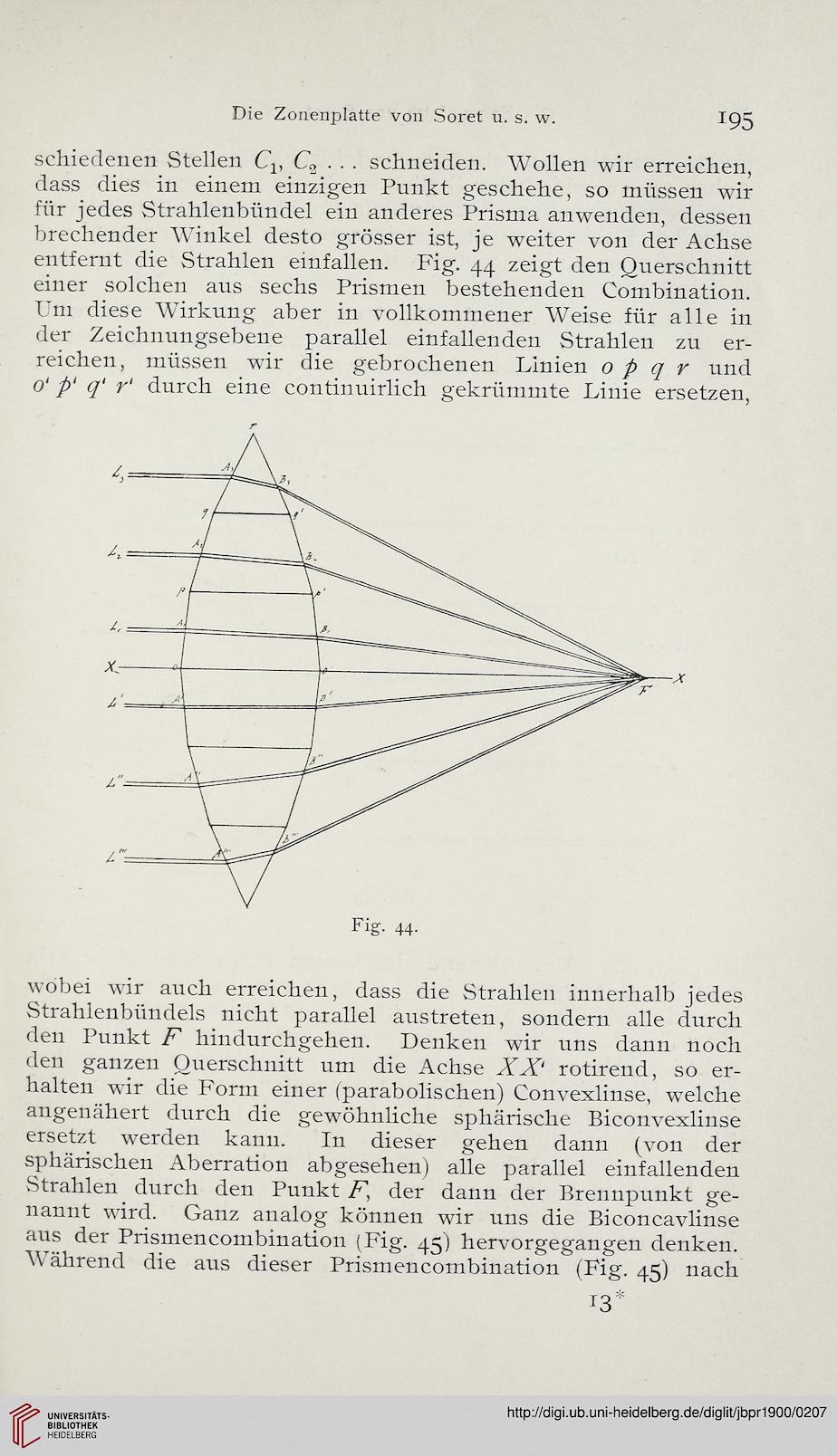
entfernt die Strahlen einfallen. Fig. 44 zeigt den Querschnitt
einer solchen aus sechs Prismen bestehenden Combination.
Um diese Wirkung aber in vollkommener Weise für alle in
der Zeichnungsebene parallel einfallenden Strahlen zu er-
reichen, müssen wir die gebrochenen Linien o p q r und
0' p‘ q' r‘ durch eine continuirlich gekrümmte Linie ersetzen,
wobei wir auch erreichen, dass die Strahlen innerhalb jedes
Strahlenbündels nicht parallel austreten, sondern alle durch
den Punkt F hindurchgehen. Denken wir uns dann noch
den ganzen Querschnitt um die Achse XX' rotirend, so er-
halten wir die Form einer (parabolischen) Convexlinse, welche
angenähert durch die gewöhnliche sphärische Biconvexlinse
ersetzt werden kann. In dieser gehen dann (von der
sphärischen Aberration abgesehen) alle parallel einfallenden
Strahlen durch den Punkt F, der dann der Brennpunkt ge-
nannt wird. Ganz analog können wir uns die Biconcavlinse
aus der Prismencombination (Fig. 45) hervorgegangen denken.
Während die aus dieser Prismencombination (Fig. 45) nach
T95
schiedenen Stellen Q, C2 ■ ■ ■ schneiden. Wollen wir erreichen,
dass dies in einem einzigen Punkt geschehe, so müssen wir
für jedes Strahlenbündel ein anderes Prisma anwenden, dessen
brechender Winkel desto grösser ist, je weiter von der Achse
entfernt die Strahlen einfallen. Fig. 44 zeigt den Querschnitt
einer solchen aus sechs Prismen bestehenden Combination.
Um diese Wirkung aber in vollkommener Weise für alle in
der Zeichnungsebene parallel einfallenden Strahlen zu er-
reichen, müssen wir die gebrochenen Linien o p q r und
0' p‘ q' r‘ durch eine continuirlich gekrümmte Linie ersetzen,
wobei wir auch erreichen, dass die Strahlen innerhalb jedes
Strahlenbündels nicht parallel austreten, sondern alle durch
den Punkt F hindurchgehen. Denken wir uns dann noch
den ganzen Querschnitt um die Achse XX' rotirend, so er-
halten wir die Form einer (parabolischen) Convexlinse, welche
angenähert durch die gewöhnliche sphärische Biconvexlinse
ersetzt werden kann. In dieser gehen dann (von der
sphärischen Aberration abgesehen) alle parallel einfallenden
Strahlen durch den Punkt F, der dann der Brennpunkt ge-
nannt wird. Ganz analog können wir uns die Biconcavlinse
aus der Prismencombination (Fig. 45) hervorgegangen denken.
Während die aus dieser Prismencombination (Fig. 45) nach